Inside the Ivy Bridge and Haswell BTB

After last time’s analysis of the Arrendale BTB, I thought I should take a look at more contemporary CPUs. At work I have access to Haswell and Ivy Bridge machines. Before I got too far into interpretation, I spent a while making it as easy as possible to remotely run tests, and graph. The code has improved a little in this regard. For completeness, this article was written with the code at SHA hash ab8cbd1d.

The Ivy Bridge I tested was an E5 2667v2 and the Haswell was an E5 2697v3.

Total size

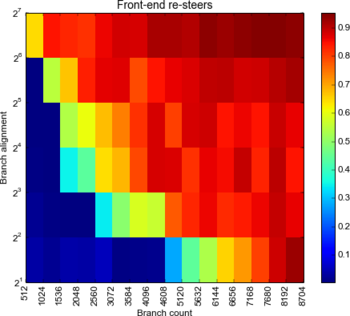
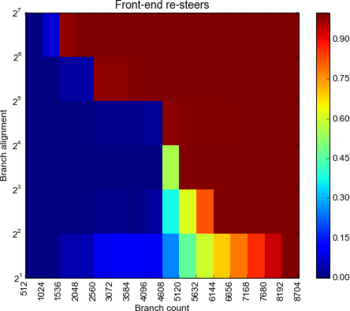
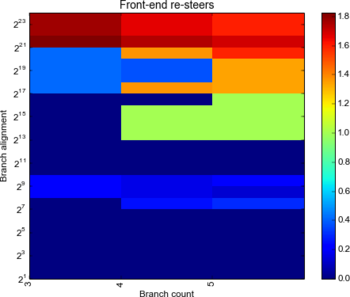
First up let’s try and see how many branches we can fit in the BTB:

There’s a marked difference between Ivy and Haswell here: although they both seem to max out with 4096 entries (the largest number of branches we can have without any resteers), the Haswell keeps a great resteerless track record up to branches 2⁴ bytes apart. The Ivy shows similar results to the Arrendale inasmuch as it quickly degrades as the branches space out.

This seems to hint to a larger set associativity on the Haswell, or a very different set index determination strategy where branches are more evenly attributed to sets even when widely spaced.

Verdict: Ivy and Haswell both have 4096 BTB entries.

Number of ways

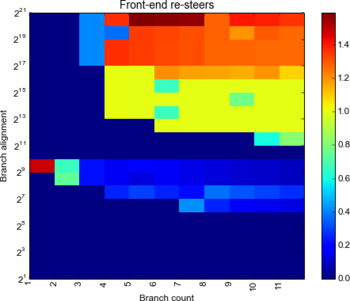
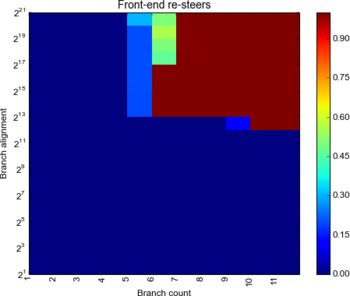
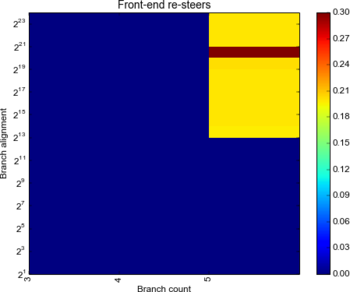
Let’s try and work out the number of ways the sets have:

The Ivy seems to 4-way set associative: we can always fit in 4 branches landing in the same set (we assume!). The Haswell on the other hand seems to be 5-way - on the sixth way we see 90+% resteers, but only 20% at 5-way. A 5-way set seems very unlikely: instead my guess is there’s a smarter replacement policy than “LRU” and a 4-way set. One guess is that somehow when all four ways are filled with “hot” branches, the 5th branch is not allowed to evict the others and is just flatly mispredicted, yielding a 1 in 5 (20%) misprediction rate. Or that a random entry is evicted giving a similar result. Either way, the pathological case of N+1 branches landing in the same set seems to no longer happen.

Verdict: Both have 4 ways; Haswell is much smarter about replacing them.

Set determination bits

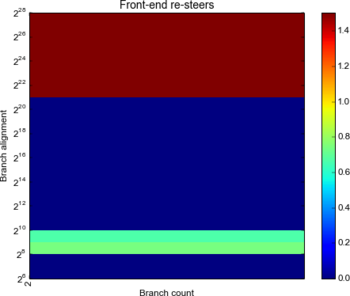
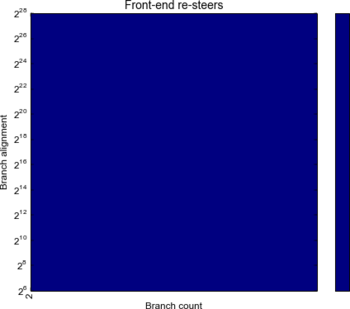
So, we suspect Haswell is using a different strategy to determine which set an address maps to. Let’s take a look at resteers for 3, 4 and 5 branches with a big D, to see if we can draw any conclusions:

Well, a real difference. Ivy is still seemingly using the lower-order bits (4 through 12 in this case) to determine set – we see resteers coming in for 4 branches once the addresses only differ in bits 13 and above. There’s a little unusual behaviour in bits 16, 18, 19 and 20, possibly associated with more of an address hash like I suspect on Arrendale.

It’s a whole other picture for Haswell: no discernable resteers at all! Just the 20% resteers at 5 branches we’d expect given the seemingly improved eviction setup.

This really points to a completely new mechanism for set determination. I’ll dig into this next time I think.

Verdict: Ivy is pretty much the same as Arrendale. Haswell is using something totally new for set determination.

Address tag bits

The last of my canned tests is to see which bits of the address is stored in the tag. Similar to the set determination we use a small number (in this case two) of branches and space them out to see if we can get them to collide:

Again Ivy looks pretty much the same as Arrendale: bits 21+ don’t seem to be used in the tag.

For Haswell it’s less clear: given that we don’t know how the sets are mapped it’s not obvious that we’re landing two branches in the same set ever: No resteers at all were recorded in this test.

Verdict: Ivy uses the same tag bits as Arrendale. Haswell cannot be determined.

Conclusions

From these results, it seems Ivy Bridge (and therefore probably Sandy Bridge) uses pretty much the same strategy for BTB lookups of unconditional branches, albeit with a larger table size: 4096 entries split over 1024 sets of 4 ways.

For Haswell it seems a new approach for determining sets has been taken, along with a new approach to evicting entries.

I’m going to dig further into the set determination next time.