The BTB in contemporary Intel chips
I’m in the middle of an investigation of the branch predictor on modern Intel chips. Read the previous article to get some background, and the first part for an overview of branch prediction.
This time I’m digging into the branch target buffer (BTB) on my Arrendale laptop (Core i5 M 520, model 37 stepping 5).
The branch target buffer hints to the front-end that a branch is coming, before the instructions have even been fetched and decoded. It caches the destination and some information about the branch – whether it’s conditional, for example. It’s thought to be a cache-like structure, that has been hinted to be multi-level, like the memory caches. I wanted to find out how big the BTB is and how it was organized.
For this test I broadly used the same approach as Vladimir Uzelac’s thesis, wihch is to create a sequence of N branches, each aligned to a particular boundary D. By varying N and D and looking at some of the microarchitectural counters, it should be possible to work out the BTB arrangement.
The assumption is that some of the branch address bits are used to pick one of the sets. Then a matching entry is searched for across the ways of that set using a tag comprised of a different subset of the branch address bits. For example, one might use bits 4-10 of the branch address to select one of 128 sets, and then search among the ways using bits 11-24 as the tag. It is assumed that the BTB doesn’t store every single address bit in the tag to save space.
In order to remove any taken/not-taken noise from this study, I used unconditional branches. I used the following counters (c.f. the Intel manual, pages 362+), in addition to the CPU cycles counter:
| Event num | Mask | Name | Description |
|---|---|---|---|
| e6 | 1f | Front-end resteers | Counts the number of times the front end is resteered, mainly when the Branch Prediction Unit cannot provide a correct prediction and this is corrected by the Branch Address Calculator at the front end. This can occur if the code has many branches such that they cannot be consumed by the BPU. Each BACLEAR asserted by the BAC generates approximately an 8 cycle bubble in the instruction fetch pipeline. The effect on total execution time depends on the surrounding code. |
| e8 | 01 | Early BPU clears | Counts early (normal) Branch Prediction Unit clears: BPU predicted a taken branch after incorrectly assuming that it was not taken. The BPU clear leads to 2 cycle bubble in the Front End. |
| e8 | 02 | Late BPU clears | Counts late Branch Prediction Unit clears due to Most Recently Used conflicts. The BPU clear leads to a 3 cycle bubble in the Front End. |
My hope is the e6:1f event will tell me whenever the branch address calculator (BAC) in the decoder notices a branch that the BTB hadn’t already spotted. This should be a pretty good indication that the BTB was missing any information for a particular branch. The other two counters turned out not to be as diagnostic and I don’t show the results below except in the detailed view (click the images below for that).
For each experiment, I ran 100 times and took the run that had the minimum number of front-end resteers.
Total size of the BTB
First up I tried to work out the total number of entries in the BTB. For this I varied N between 512 and 8704 in steps of 512 and tried a few low values of D. The results are as follows:
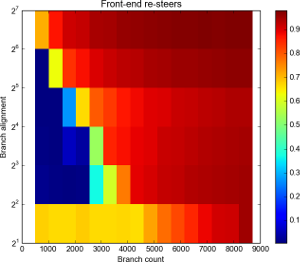
Resteers by branch count and alignment. Click for full details.
Alignment is log scale.
As you can see, for D=2 there’s a lot of resteers. At D=2 there’s no distance at all between the jump instructions – they’re 2 bytes each – and the BTB is inundated. Assuming a “line size” of 16 or 32 bytes, we’re putting either 8 or 16 branches in each BTB line. That seems to be enough to flood it completely, overwhelming the ways and causing a resteer pretty much every branch, though it gradually goes up from a 75% resteer rate to 100% between around the 4096 to 8192 mark.
At D=4, the branch density is more sensible and we see fewer than 1% resteers up to and including 2048 branches, then 37% misses at N=2560, rising to 90% at N=4096. The results are similar for D=8. At D=16 there’s around 27% at 1536, 60% at 2048.
At D=32 and D=64 we’re starting to see significant resteering at the 512 and 1024 mark, respectively.
My interpretation is that there are 2048 entries in the BTB: 2048 is the greatest number of branches we were able to have with no significant resteers (at D=4 and D=8).
For the D=4 case, at N=2560 we’d expect 2560-2048=512 of the BTB entries to overspill. If we assume a simple least-recently-used replacement strategy we’d expect the overspill to be pathological: each overspilling branch kicks out the next branch due to execute…which kicks out the next and so on.
This would lead us to expect (ways+1) * 512 evictions. We see 37% evictions – which implies only 1 way ((1 + 1) * 512 / 2560 = 40%). At 3072 we see 59% – with only one way, we’d expect 80% ((1 + 1) * 1024 / 2560). This seems contradictory, and one way seems unlikely anyway. The replacement policy is probably not as simple as LRU. We’ll try to come back to this another time.
As D increases we reach the point where we’re not picking every possible set: If the set choice is (for example) bits 4 and above, then at D=32 we are missing every other set, which halves the number of entries that are available to us. This could explain the results for D=32 and above.
Number of ways
Next up was trying to determine the number of ways. For this I used a small number of branches, spaced a long way apart to try and ensure each branch lands back in the same set. That way we should be able to find the number of branches which fit in one set, as well as get some idea on how the branch addresses map to sets.
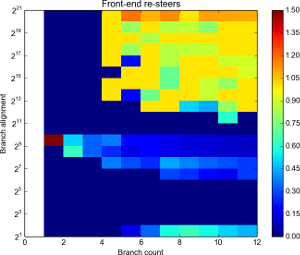
Resteers by branch count and alignment. Click for full details.
Alignment is log scale.
This is a fun one. Ignoring the somewhat odd behaviour around D=256 and D=512 it seems pretty clear that there BTB is 4-way: we can always fit at least four branches without resteers.
With D less than 4096 (212) it seems we aren’t landing back in the same set: there aren’t so many resteers (less than 50% in the main), compared to the near 100% rate at 4 branches above that. D of 4096 and above seems to bring out the worst of the BTB. This seems to implies the set is determined by bits 0-11 only.
Assuming 4-ways, and 2048 entries, that implies 2048/4 = 512 sets. 512 sets means 9 address bits. Given the fact that bits 12+ don’t seem to be used, it would seem likely that bits 3-11 of the branch address are used to pick the set.
That said: a closer look at the results seems to suggest something more clever is happening. Note the lack of resteers at branch count 4 at D=215, and the relatively few resteers at count 5 D=216. Also interesting is the fact we seem to be able to get 5 branches at D=212. Another oasis of few resteers is at N=8 and N=9 at D=212.
To me this suggests that it’s not a simple mapping from address to set: I’m beginning to suspect there’s some “hash” going on involving bits 12, 13, 15 adn 16 as well as possibly bits 8 and 9 (explaining the oddity at D=256 and D=512).
More investigations are required – I’ll definitely be returning to this, and also trying to find more evidence to support my theories. So far I can’t see any evidence that the BTB is multi-level: from an Intel patent it seems that only the conditional instructions may use the second level.
As before the code is on GitHub, and the code was at revision 203499a84 when it was used to write this post.
In another post I’ll look at how many tag bits are used.